Autoencoder and Deep Features
In this tutorial-like kernel, using data from New York City Taxi Trip Duration, we use the autoencoder and deeplearning capability of the H2O framework to explore deep features. Such an approach provides a means of reducing features (Hinton & Salakhutdinov, 2006)—although here there is no need, for the number of features is already small. It also offers a way to leverage unlabelled data—a technique called semi-supervised learning. The kernel Diabolo Trick: Pre-train, Train and Solve gives a concrete example. Finally, it is perhaps worth noting that deep features are the backbone of some transfer learning techniques.
Features Tinkering
First, we remove the column dropoff_datetime, as otherwise there is no point to predict the duration of the trip… We could just precisely calculate it…
X[, dropoff_datetime := NULL]
Outliers
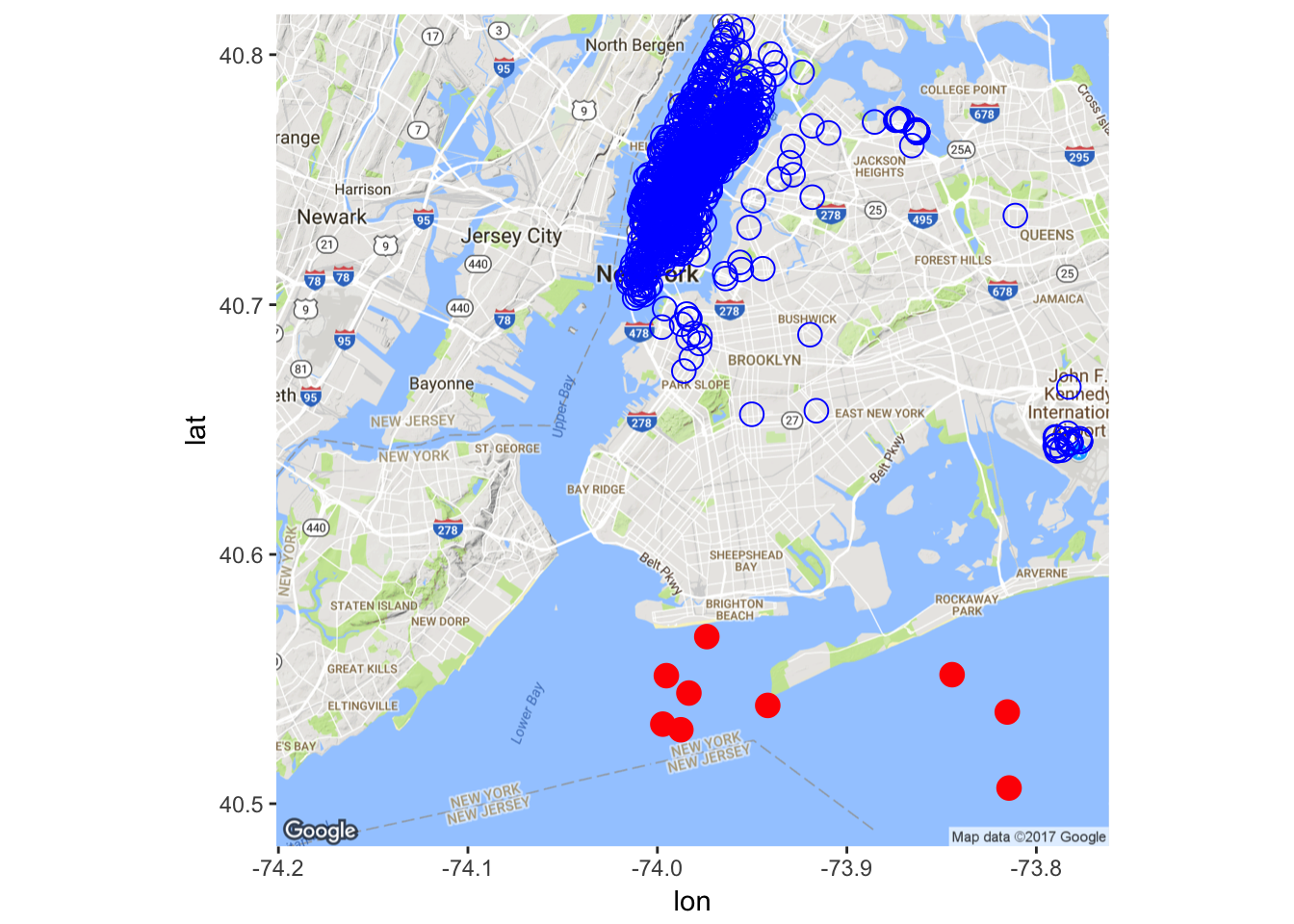
Pickup Location
There seems to be some outliers in the dataset. Let’s remove some of them (obviously, a better way should be devised here, for the current naive implementation misses some outliers while removing some non-outliers).
X <- X[-which(X$pickup_longitude > -74
& X$pickup_latitude < 40.57), ]
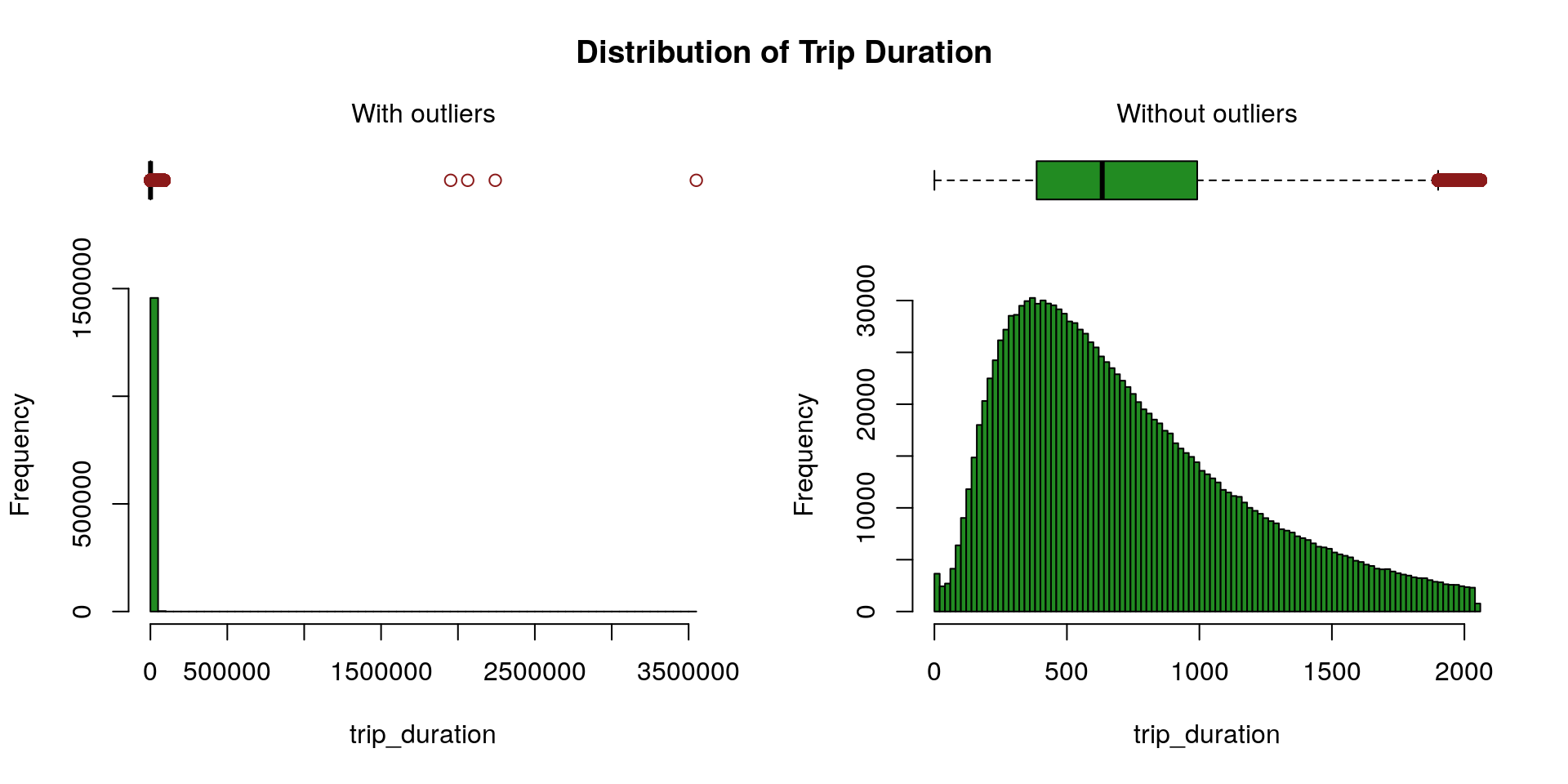
Trip Duration
We rely on the Hampel’s test to compute the maximum threshold above which values are declared spurious. One can find further details about the Hampel’s test for outlier detection in Scrub data with scale-invariant nonlinear digital filters.
X <- X[-which(X$trip_duration > maxThreshold), ]
Locations and Distances
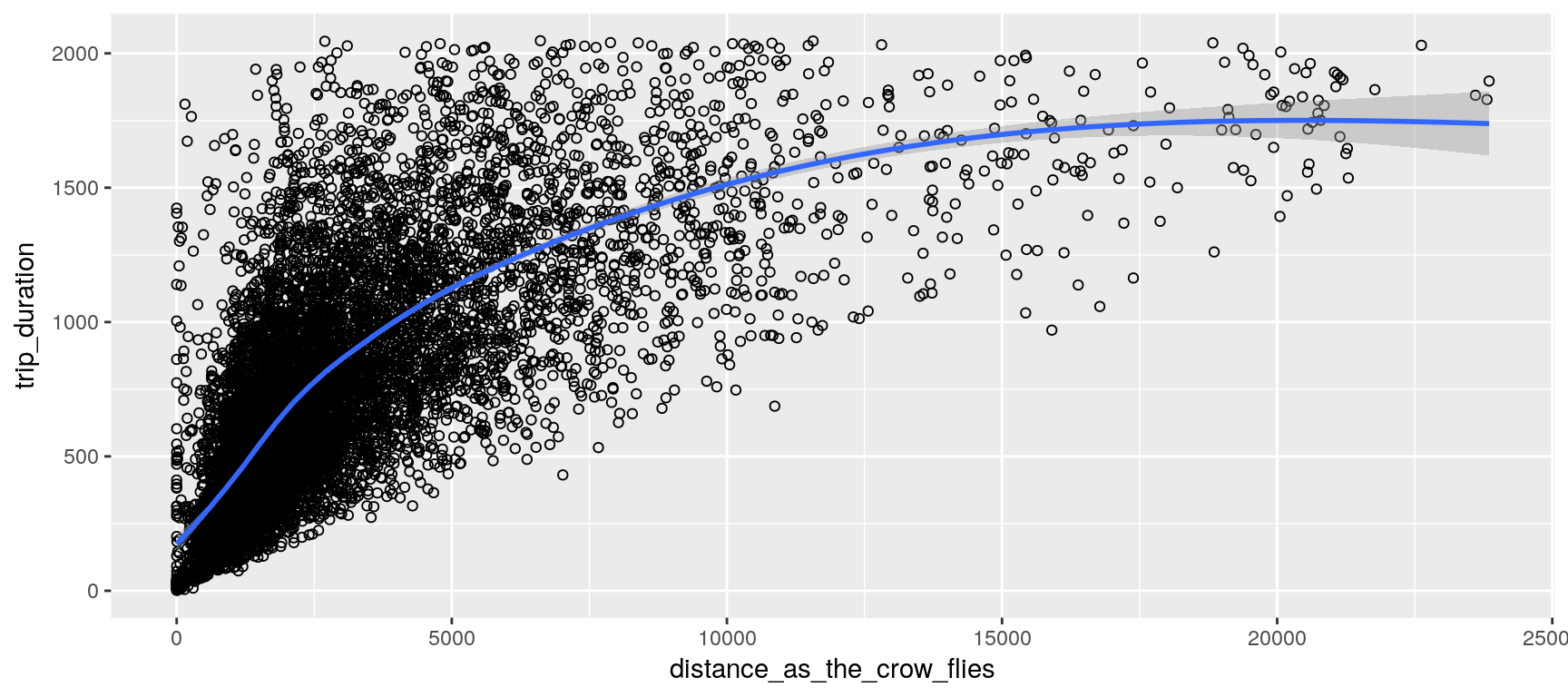
We assume that the earth’s surface forms a perfect sphere; so that we can conveniently use the haversine formula to estimate each trip distance as the crow flies. (This distance should constitute a rough estimation of the covered distance; at least it gives a minimum.)
X[, distance_as_the_crow_flies := distHaversine(
data.table(pickup_longitude, pickup_latitude),
data.table(dropoff_longitude, dropoff_latitude))]
Xt[, distance_as_the_crow_flies := distHaversine(
data.table(pickup_longitude, pickup_latitude),
data.table(dropoff_longitude, dropoff_latitude))]
Pickup Date
We add the two new features wday and hour.
X[, pickup_datetime := fastPOSIXct (pickup_datetime, tz = "EST")]
X[, wday := wday(pickup_datetime)]
X[, hour := hour (pickup_datetime)]
Xt[, pickup_datetime := fastPOSIXct (pickup_datetime, tz = "EST")]
Xt[, wday := wday(pickup_datetime)]
Xt[, hour := hour (pickup_datetime)]
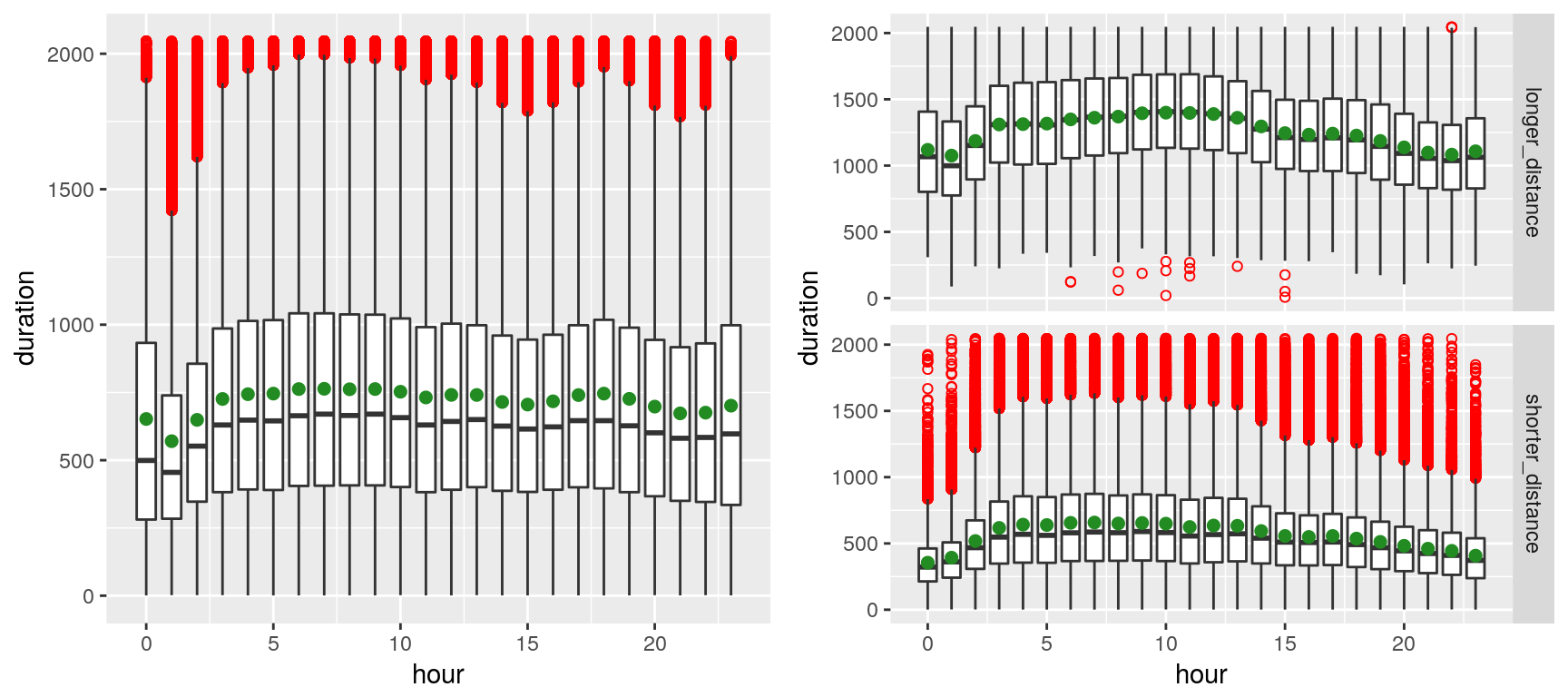
We can observe, on the left plot, the presence of outliers (red dots)—which markedly shift the mean (green spot) from the median—presumably due to the volatility of the traffic in New York. The right plot contrasts shorted distances (arbitrarily chosen as less than 4 Km) with longer distances. Outliers appear to merely plague the shorter distances (which is fairly intuitive, especially given that many of the shorter-distance trips appear to be within Manhattan).
The plot above suggests that trip durations are longer late at night during the weekend, whereas they tend to be longer early morning (4~8) during the weekdays (depicting the rush hours of commuters). That sounds rather unsurprising…
Convert Categorical Variables to Numerical
There is 1 categorical variables, and there are 9 numerical variables with non-null standard deviation.
X[, store_and_fwd_flag := ifelse (store_and_fwd_flag == "N", 0, 1)]
Deep Features
Convert to H2O Frames
if (kIsOnKaggle) {
# we reduce the training set size to avoid time out
set.seed(1)
trainIndexes <- createDataPartition(
y = X[["trip_duration"]], p = 0.1, list = FALSE)
X <- X[trainIndexes, ]
rm(trainIndexes)
}
train <- as.h2o(X)
predictors <- setdiff (names(X), c(toIgnore))
Autoencoder (Diabolo Network)
if (kIsOnKaggle) {
hyperParamsAutoencoder = list(
hidden = list(c(8, 4, 8), c(8, 3, 8), c(7, 3, 7), c(6, 3, 6)),
activation = c("Tanh"))
} else {
hyperParamsAutoencoder = list(
hidden = list(c(11, 8, 11), c(10, 8, 10), c(9, 5, 9), c(8, 5, 8),
c(7, 5, 7), c(6, 5, 6), c(11, 7, 11), c(10, 7, 10),
c(9, 4, 9), c(8, 4, 8), c(7, 4, 7), c(6, 4, 6),
c(11, 6, 11), c(10, 6, 10), c(9, 3, 9), c(8, 3, 8),
c(7, 3, 7), c(6, 3, 6), c(11, 5, 11), c(10, 5, 10),
c(11, 4, 11), c(10, 4, 10), c(11, 8, 5, 8, 11)),
activation = c("Tanh"))
}
gridAutoencoder <- h2o.grid(
x = predictors,
autoencoder = TRUE,
training_frame = train,
hyper_params = hyperParamsAutoencoder,
search_criteria = list(strategy = "Cartesian"),
algorithm = "deeplearning",
grid_id = "grid_autoencoder",
reproducible = TRUE,
seed = 1,
variable_importances = TRUE,
categorical_encoding = "AUTO",
score_interval = 10,
epochs = 800,
adaptive_rate = TRUE,
standardize = TRUE,
ignore_const_cols = FALSE)
The following table summarizes the grid results (it is sorted increasingly by ‘mse’):
| activation | hidden | mse | |
|---|---|---|---|
| 1 | Tanh | [8, 4, 8] | 2.2115573249558083E-5 |
| 2 | Tanh | [8, 3, 8] | 6.43305860410787E-4 |
| 3 | Tanh | [7, 3, 7] | 6.519543824901826E-4 |
| 4 | Tanh | [6, 3, 6] | 6.730825397209355E-4 |
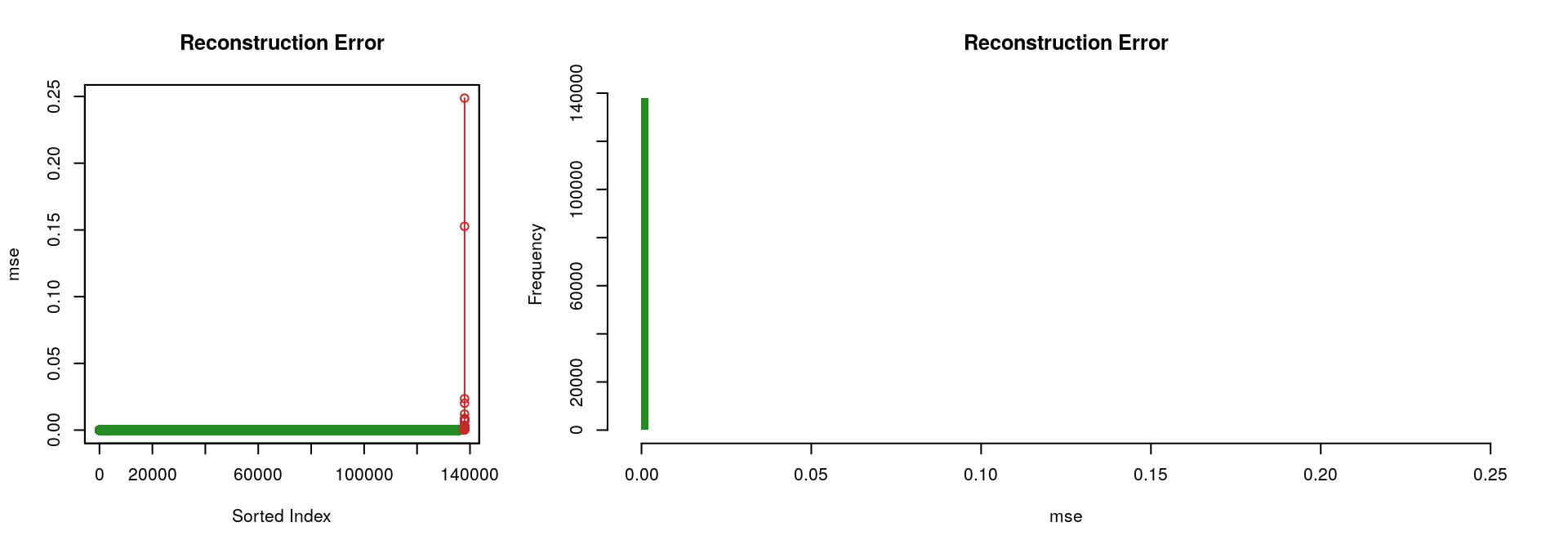
Considering the “best” autoencoder (i.e., the one with the lowest ‘mse’, which is the one with the hidden layers [8, 4, 8]), the two following figures illustrate the fact that it performs rather well; only a limited portion of the input signal could not be reconstructed.
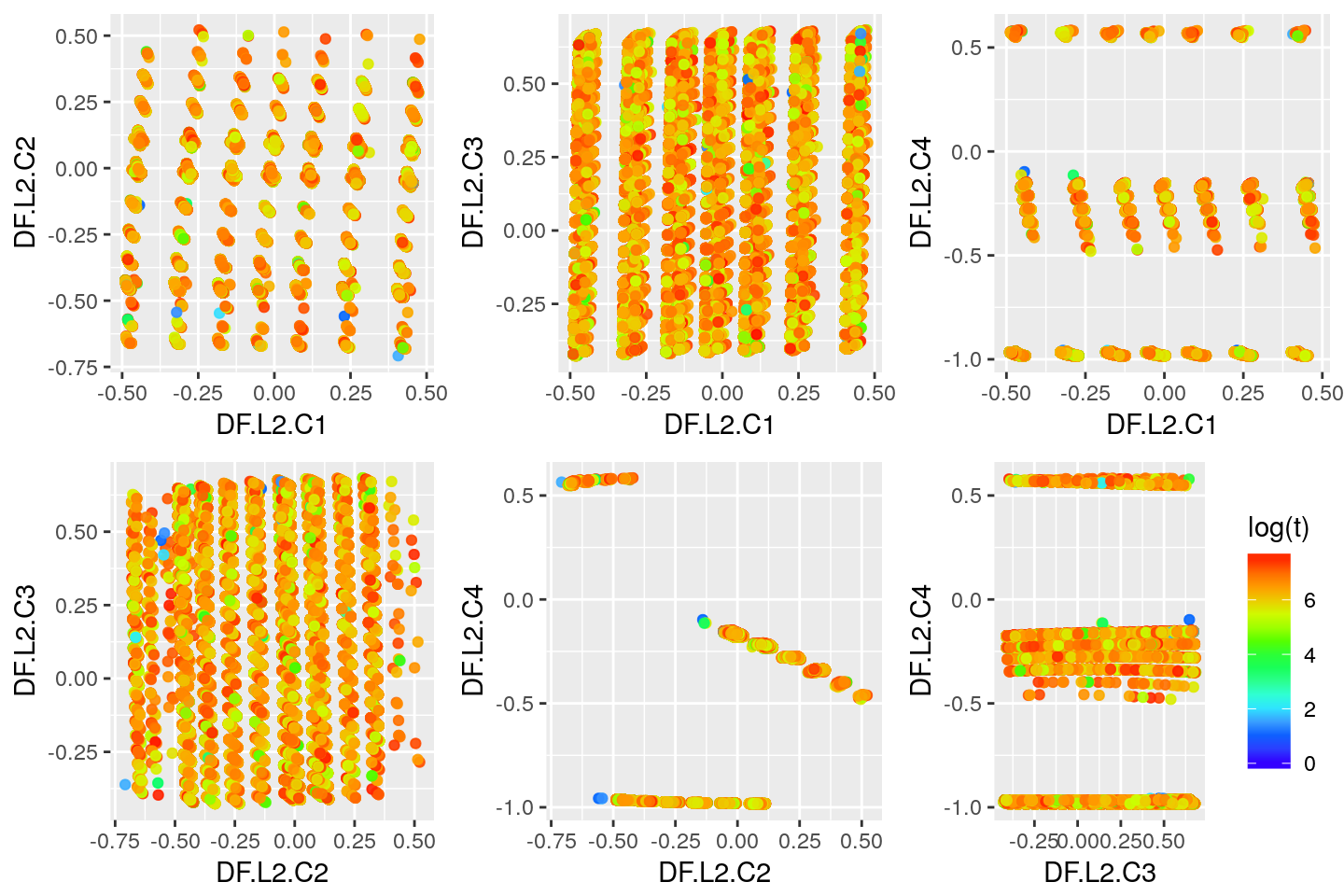
Deep Features Visualization
Second Layer
layer <- 2
deepFeature2 <- h2o.deepfeatures(bestAutoencoder, train, layer = layer)
data <- as.data.frame(deepFeature2)
data$log_trip_duration <- log(X$trip_duration)
summary(data)
## DF.L2.C1 DF.L2.C2 DF.L2.C3 DF.L2.C4
## Min. :-0.48997 Min. :-0.70796 Min. :-0.4266 Min. :-0.9829
## 1st Qu.:-0.28532 1st Qu.:-0.45367 1st Qu.:-0.1012 1st Qu.:-0.9661
## Median :-0.05116 Median :-0.04050 Median : 0.1981 Median :-0.9644
## Mean :-0.05273 Mean :-0.18749 Mean : 0.1545 Mean :-0.5969
## 3rd Qu.: 0.12783 3rd Qu.:-0.01238 3rd Qu.: 0.4004 3rd Qu.:-0.1662
## Max. : 0.47711 Max. : 0.52161 Max. : 0.6832 Max. : 0.5846
## log_trip_duration
## Min. :0.000
## 1st Qu.:5.951
## Median :6.446
## Mean :6.376
## 3rd Qu.:6.894
## Max. :7.624
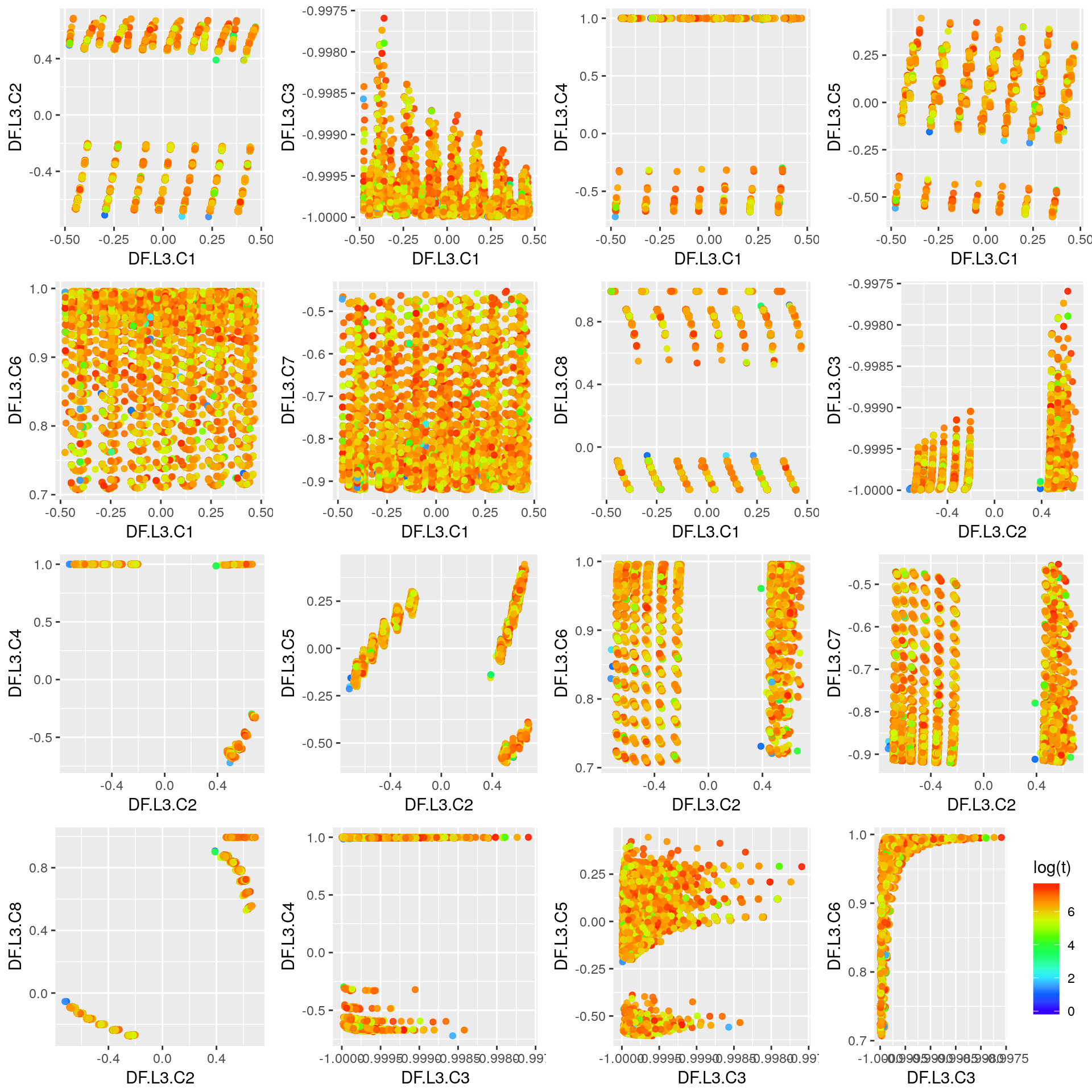
Third Layer
layer <- 3
deepFeature3 <- h2o.deepfeatures(bestAutoencoder, train, layer = layer)
data <- as.data.frame(deepFeature3)
data$log_trip_duration <- log(X$trip_duration)
summary(data)
## DF.L3.C1 DF.L3.C2 DF.L3.C3 DF.L3.C4
## Min. :-0.47818 Min. :-0.72271 Min. :-1.0000 Min. :-0.7213
## 1st Qu.:-0.14682 1st Qu.:-0.66474 1st Qu.:-1.0000 1st Qu.: 0.9941
## Median : 0.02289 Median :-0.32626 Median :-0.9999 Median : 0.9997
## Mean : 0.03259 Mean :-0.09229 Mean :-0.9998 Mean : 0.9889
## 3rd Qu.: 0.26142 3rd Qu.: 0.46748 3rd Qu.:-0.9998 3rd Qu.: 0.9997
## Max. : 0.47005 Max. : 0.68681 Max. :-0.9976 Max. : 1.0000
## DF.L3.C5 DF.L3.C6 DF.L3.C7 DF.L3.C8
## Min. :-0.60460 Min. :0.7071 Min. :-0.9202 Min. :-0.27290
## 1st Qu.:-0.12264 1st Qu.:0.8905 1st Qu.:-0.8631 1st Qu.:-0.09507
## Median :-0.03823 Median :0.9506 Median :-0.8037 Median :-0.09062
## Mean :-0.03506 Mean :0.9294 Mean :-0.7637 Mean : 0.33366
## 3rd Qu.: 0.01698 3rd Qu.:0.9848 3rd Qu.:-0.6714 3rd Qu.: 0.87194
## Max. : 0.44521 Max. :0.9960 Max. :-0.4528 Max. : 0.99467
## log_trip_duration
## Min. :0.000
## 1st Qu.:5.951
## Median :6.446
## Mean :6.376
## 3rd Qu.:6.894
## Max. :7.624
Predictions Using Deep Features and GBM
We use the second layer of the autocencoder (bestAutoencoder) and the gradient boosting machine algorithm offered by H2O (h2o.gbm). Those are arbitrary choices for the purpose of exemplifying a use of deep features.
layer <- 2
Get Deep Features & Split Data
deepFeatureTrain <- h2o.deepfeatures(bestAutoencoder, train, layer = layer)
deepFeatureTrain[["trip_duration"]] <- as.h2o(X$trip_duration)
splits <- h2o.splitFrame(
data = deepFeatureTrain,
ratios = c(0.7),
seed = 1
)
trainDf <- splits[[1]]
validDf <- splits[[2]]
Grid Search
deepfeatures <- setdiff(names(deepFeatureTrain), c("trip_duration"))
if (kIsOnKaggle) {
hyperParamsGbm <- list(
max_depth = c(3, 4),
min_split_improvement = c(0, 1e-6))
} else {
hyperParamsGbm <- list(
max_depth = seq(3, 15, 2),
sample_rate = seq(0.2, 1, 0.01),
col_sample_rate_per_tree = seq(0.2, 1, 0.01),
col_sample_rate_change_per_level = seq(0.6, 1.4, 0.02),
min_rows = 2^seq(0, log2(nrow(train))-3, 1),
nbins = 2^seq(2, 10, 1),
nbins_cats = 2^seq(1, 4, 1),
histogram_type = c("UniformAdaptive", "QuantilesGlobal", "RoundRobin"),
min_split_improvement = c(0, 1e-8, 1e-6, 1e-4))
}
gridGbm <- h2o.grid(
hyper_params = hyperParamsGbm,
search_criteria = list(strategy = "Cartesian"),
algorithm = "gbm",
grid_id = "grid_gbm",
x = deepfeatures,
y = "trip_duration",
training_frame = trainDf,
validation_frame = validDf,
nfolds = 0,
ntrees = ifelse(kIsOnKaggle, 200, 1000),
learn_rate = 0.05,
learn_rate_annealing = 0.99,
max_runtime_secs = ifelse(kIsOnKaggle, 120, 3600),
stopping_rounds = 5,
stopping_tolerance = 1e-5,
stopping_metric = "MSE",
score_tree_interval = 10,
seed = 1,
fold_assignment = "AUTO",
keep_cross_validation_predictions = FALSE)
sortedGridGbm <- h2o.getGrid("grid_gbm", sort_by = "mse", decreasing = TRUE)
| max_depth | min_split_improvement | mse | |
|---|---|---|---|
| 1 | 3 | 1.0E-6 | 187782.15952044743 |
| 2 | 3 | 0.0 | 187782.15952044743 |
| 3 | 4 | 0.0 | 183708.52366487522 |
| 4 | 4 | 1.0E-6 | 183708.52366487522 |
Best Model & Performance on the Validation Set
bestGbmModel <- h2o.getModel(sortedGridGbm@model_ids[[1]])
perf <- h2o.performance(bestGbmModel, newdata = validDf)
## H2ORegressionMetrics: gbm
##
## MSE: 187782.2
## RMSE: 433.3384
## MAE: 349.3986
## RMSLE: 0.7301732
## Mean Residual Deviance : 187782.2
Retrain the Best Model Using the Entire Train Set
Here we use k-folds cross validation to evaluate the final model (trained using the entire train set—i.e., rbind(trainDf, validDf)).
nfolds <- ifelse(kIsOnKaggle, 2, 8)
finalModel <- do.call(h2o.gbm,
{
p <- bestGbmModel@parameters
p$model_id = NULL
p$training_frame = h2o.rbind(trainDf, validDf)
p$validation_frame = NULL
p$nfolds = nfolds
p
})
finalModel@model$cross_validation_metrics_summary
## Cross-Validation Metrics Summary:
## mean sd cv_1_valid cv_2_valid
## mae 350.8387 0.10633527 350.68832 350.9891
## mean_residual_deviance 189029.88 113.88638 188868.83 189190.94
## mse 189029.88 113.88638 188868.83 189190.94
## r2 0.029764593 1.9335767E-4 0.030038042 0.029491143
## residual_deviance 189029.88 113.88638 188868.83 189190.94
## rmse 434.77563 0.13097145 434.5904 434.96085
## rmsle 0.73611194 0.0039748037 0.73049074 0.7417332
Test Set & Submission
deepFeatureTest <- h2o.deepfeatures(bestAutoencoder, test, layer = layer)
deepFeatureTest[["trip_duration"]] <- as.h2o(Xt$trip_duration)
pred <- h2o.predict (finalModel, newdata = deepFeatureTest)
fwrite(data.table(id = Xt$id, trip_duration = as.vector(pred$predict)),
file = file.path(".", paste0("output-gbm-", Sys.Date(), ".csv"),
fsep = .Platform$file.sep),
row.names = FALSE, quote = FALSE)
Remark
In general, using the top model out of the grid search might not be the wisest approach. Instead, considering the k best models might yield improved performances (k > 1). An easy way to use k models is to average their predicted probabilities. A more sophisticated way consists in using ensemble learning (super learner), for which the choice of the meta-learner can help to even further improve the result (e.g., see H2O’s documentation on Stacked Ensembles).
Predictions Using Pretrained Neural Networks
This section describes an alternative approach to the previous section and is presented in a dedicated kernel: Deep Semi-supervised Learning. ■
License and Source Code
© 2017 Loic Merckel, Apache v2 licensed. The source code is available on both Kaggle and GitHub.
References
- Hinton, G. E., & Salakhutdinov, R. R. (2006). Reducing the Dimensionality of Data with Neural Networks. Science, 313(5786), 504–507. https://goo.gl/6GjADx